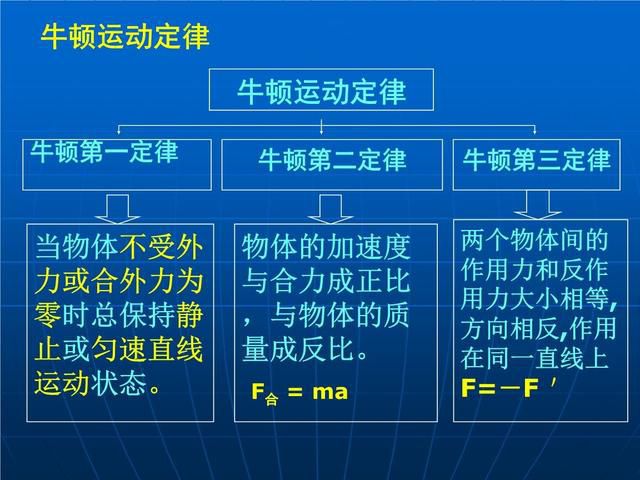
為了驗證地面上的引力與地球吸引月球、太陽吸引行星的力是同一種力,遵循同一規律,牛頓進行了著名的“月地”試驗。其基本思想是:如果引力與天體間的引力是同一種力,且都與距離的平方成正比,那么月球繞地球做近似圓周運動的向心加速度應該是地面引力加速度的1/3600,因為月球中心到地心的距離是地球半徑的60倍。牛頓通過計算證明了自己的想法是正確的。
所謂月地檢驗,是指牛頓當年思考的一個問題:月球是否也受到地球引力的影響?這種引力和地面上物體受到的引力是否相同(只是大小不同)?
推制工序:

牛頓當時所知道的數據:月球公轉周期T(T = 27.3天),月球與地球的距離R = 3.84 * 10^8米,地面附近的重力加速度g = 9.8m/s^2,地球半徑R = 6.4 * 10^6米(其實牛頓當時并不知道這個數據,他是根據水手們用的方法算出地球半徑的)

1.如果月球繞地球做圓周運動的向心力是由引力提供的,那么它的向心加速度a=GM/R2=g*R^2/R^2=9.8*(6.4*10^6)^2/(3.84*10^8)^2m/s^2=2.72*10^(-3)m/s^2

(GM=g*R^2,即黃金替代公式月球引力常數,M為地球質量,G為引力常數)
2、根據月球繞地球的圓周運動月球引力常數,可得向心力公式為:
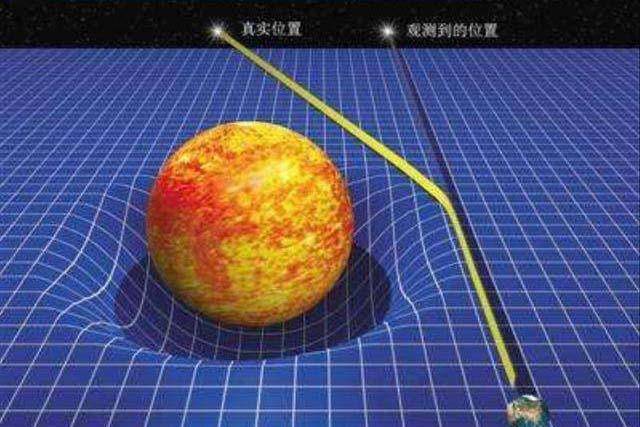
a=2πR/T)^2/R=4π^2R/T^2=4*π^2*3.84*10^8/(27.3*24*3600)^2米/秒^2=2.74*10^(-3)米/秒^2
兩種方法得到的向心加速度在誤差范圍內是相同的。
這樣,牛頓的猜想就被檢驗了。
 名師輔導
環球網校
建工網校
會計網校
新東方
醫學教育
中小學學歷
名師輔導
環球網校
建工網校
會計網校
新東方
醫學教育
中小學學歷